Des éoliennes invisibles
Les projets d’éoliennes en mer se multiplient de nos jours. Le problème, c’est que ces constructions gâchent le paysage. Elles sont à chaque fois trop près des côtes. Pourtant, si on les met suffisamment loin, du fait de la courbure de la Terre, elle deviennent invisibles depuis la plage.
Mais à quelle distance faut-il alors les construire ? Et bien cela dépend de la hauteur maximale de l’éolienne. Prenons celles du parc de Saint Nazaire. La hauteur maximale avec le mât et le pied, et quand la pale du haut est à la verticale est de 210 mètres de haut. Mais 30 mètres du socle sont immergés. Il nous reste une hauteur émergée de 180m.
Pour calculer la distance d au delà de laquelle on ne les voit plus, il faut juste utiliser le petit schéma que j’ai mis en photo et se souvenir du théorème de Pythagore.
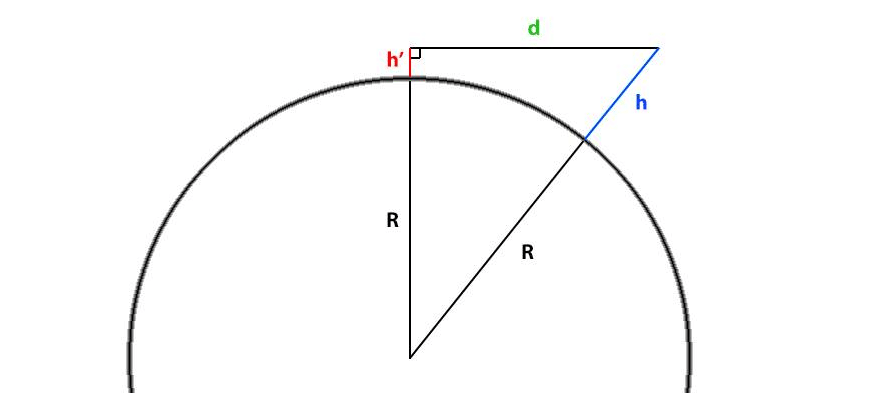
Ici, on aurait l’équation suivante :
(R+h)² = (R+h’)² + d²
Ce qui se développe comme ça : R²+2Rh+h² = R²+2Rh’+h’² + d²
En simplifiant les R², ça nous donne : d = √(2Rh+h²-2Rh’-h’²)
Avec R = le rayon de la Terre (6378km) en mètre, h la hauteur de l’éolienne en mètre et h’ la hauteur des yeux de l’observateur sur la plage.
Avec nos éoliennes de 180m de haut, ça nous donne, pour un observateur de 1.80m (et donc des yeux à environ 1.65m) :
![Rendered by QuickLaTeX.com \[\begin{aligned}d &= \sqrt{(2 \times 6\,378\,000 \times 180) + 180^2 - (2 \times 6\,378\,000 \times 1.65) - 1.65^2} \\d &= \sqrt{2\,296\,080\,000 + 32\,400 - 21\,047\,400 - 2.7225} \\d &= \sqrt{2\,275\,064\,997.2775} \\d &\approx 47\,697.64\end{aligned}\]](https://phiphou.com/wp-content/ql-cache/quicklatex.com-b0667f211ae9521d36520e6f38631506_l3.png)
Il faudrait donc placer nos éoliennes à 47.7km de la plage.
Notez que h² et h’² sont très petits face à 2Rh et 2Rh’, on peut donc les négliger et retenir la formule suivante : d=√(2Rh-2Rh’) (il n’y a que 33.96cm d’écart)