Temps π
Vous connaissez tous le nombre π. Il est le rapport entre la circonférence d’un cercle et son diamètre. Il vaut environ 3.141592.
Très tôt, les Grecs, et notamment Archimède, ont compris qu’on pouvait calculer ses décimales en utilisant une construction géométrique consistant à inscrire un polygone régulier dans un cercle. Plus votre polygone aura de côtés, plus vous pourrez obtenir un grand nombre de décimales.
C’est avec cette méthode que Ludolph van Ceulen (17ème siècle) obtiendra 35 décimales, après 20 ans de travail, en utilisant un polygone régulier à 262 côtés.
En 1706, John Machin calculera 100 décimales, en utilisant une méthode ne nécessitant pas de construction géométrique.
![\[ \frac{\pi}{4} = 4 \arctan\left(\frac{1}{5}\right) - \arctan\left(\frac{1}{239}\right) \]](https://phiphou.com/wp-content/ql-cache/quicklatex.com-e82ed961a25c82046ed7b380d88e94cf_l3.png "Rendered by QuickLaTeX.com")
L’anglais William Shanks passera plus de 20 ans à calculer 707 décimales, avec une méthode équivalente à celle de Machin, mais on découvrira plus tard que seules les 527 premières décimales étaient justes.
En 1910, le mathématicien indien Srinivasa Ramanujan proposera une formule bien plus efficace.
![\[ \frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum_{k=0}^{\infty} \frac{(4k)! \, (1103 + 26390k)}{(k!)^4 \, 396^{4k}} \]](https://phiphou.com/wp-content/ql-cache/quicklatex.com-2d91cc7a838bae1ba82e09b1f38367ee_l3.png "Rendered by QuickLaTeX.com")
En 1949, en utilisant l’ENIAC, un des premiers ordinateurs modernes (un monstre de 27 tonnes occupant une salle de 170m²), on trouvera 2037 décimales en laissant tourner la machine pendant 70 heures. Les 10000 décimales sont dépassées en 1958, en 33 heures.
En 1988, les frères Chudnovsky proposent une amélioration de la formule de Ramanujan.
![\[ \frac{1}{\pi} = \frac{12}{640320^{3/2}} \sum_{k=0}^{\infty} \frac{(-1)^k (6k)! \, (13591409 + 545140134k)} {(3k)! \, (k!)^3 \, (640320)^{3k}} \]](https://phiphou.com/wp-content/ql-cache/quicklatex.com-1d13f51509be5e307b7454957393a7cb_l3.png "Rendered by QuickLaTeX.com")
Grâce à cette formule et aux progrès phénoménaux de l’informatique dans les décennies suivantes, on attendra les 1000 milliards de décimales en 2002 (600 heures de calcul), puis en 2009 le même nombre mais en moins de 73 heures.
En mars 2019, on atteint les 31 415 926 535 897 décimales, puis 100 000 milliards de décimales en juin 2022. Le record actuel sera établi par l’équipe d’un Youtuber canadien en mai 2025, avec 300 000 milliards de décimales calculées et vérifiées en 226 jours.
Depuis 15 ans, tous ces records sont établis en utilisant le logiciel Y-cruncher écrit par Alexander Yee. Toute machine moderne peut le faire tourner.
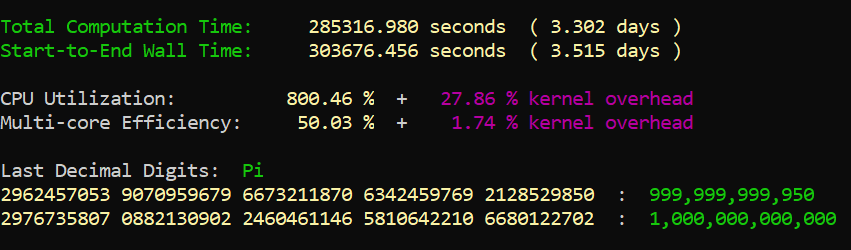
En utilisant uniquement la RAM, mon PC calcule un milliard de décimales en seulement 14.6 secondes. En utilisant mon SSD au format NVme, j’en calcule 100 milliards en seulement 2h14m24s.
Si bien qu’on peut dire que sur ce calcul, mon ordinateur (en mode RAM) est 8.47 milliards de fois plus rapide que l’ENIAC de 1949.
