Alice et Bob au RSA
Voici une petite explication simpliste de l’algorithme RSA sur lequel repose en partie la sécurité sur Internet.
Bob souhaite envoyer un message privé à Alice. Ils doivent d’abord se mettre d’accord sur le système de clef qu’ils vont utiliser.
Alice va donc créer deux clefs : une clef publique, qu’elle pourra envoyer à Bob de façon non sécurisée (c’est pour ça qu’on dit qu’elle est publique, n’importe qui pourrait y avoir accès), et une clef privée qu’elle gardera précieusement. Bob fera de même de son côté.
Ce système avec deux clefs est appelé un système asymétrique : on utilise une clef pour chiffrer un message et une autre clef, différente, pour déchiffrer le message.
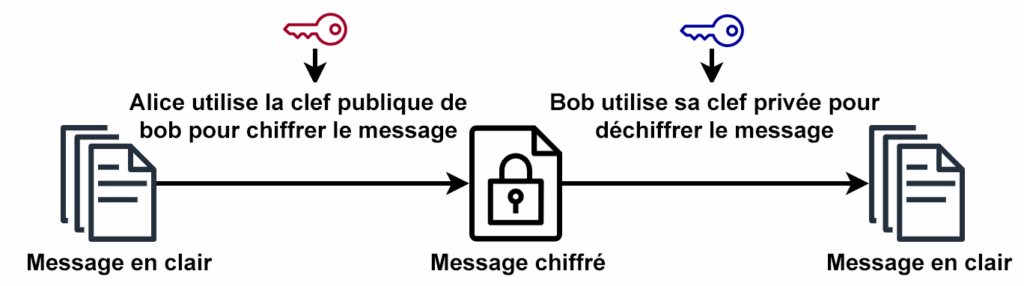
Ce système a été inventé par R. Rivest, A. Shamir et L. Adleman, d’où le nom RSA, d’après les travaux de W. Diffie et à M. Hellman.
Pour générer ces clefs, Alice va choisir deux nombres premiers distincts, notés p et q. Pour rendre notre exemple simple, on va dire qu’elle choisit p=5 et q=17. Dans la réalité, les nombres premiers en jeu sont gigantesques, ils comportent plusieurs centaines de chiffres décimaux.
Elle va maintenant calculer le produit de p et q qu’on notera n. On aura donc n = p × q. Ici, avec p=5 et q=17, on aura n=5×17=85.
Alice va aussi calculer le produit de p-1 et q-1, qu’on notera φ(n). On aura donc φ(n)=(p-1)×(q-1). Dans notre exemple, ça donnera φ(n)=(5-1)×(17-1)=4×16=64. A partir de maintenant, on peut oublier p et q, nous n’en auront plus besoin.
Elle choisira ensuite un nombre e, tel que 1 < e < φ(n) et e premier avec φ(n), c’est à dire que le PGCD de e et φ(n) est égal à 1. Dans notre exemple, nous choisirons e=3 (3 est bien compris en 1 et 64 et 3 est aussi premier avec 64).
![\[\ ax + by = \gcd(a,b)\]](https://phiphou.com/wp-content/ql-cache/quicklatex.com-8c7d55dbfa30ed25d5cfcb5009c09494_l3.png "Rendered by QuickLaTeX.com")
![\[\ a^p \equiv a \pmod{p}\]](https://phiphou.com/wp-content/ql-cache/quicklatex.com-2bc19f02cb9a35ea7edb486a7bc80e4d_l3.png "Rendered by QuickLaTeX.com")
Enfin, Alice va calculer l’inverse modulaire de e modulo φ(n) qu’on notera d. On cherche donc e tel que (d × e) est congru à 1 modulo φ(n). Pour ce faire on pourra utiliser le théorème de Bachet-Bézout, qui nous dit que ax + by = pgcd(a, b) et le petit théorème de Fermat qui nous dit que pour tout p premier, on ap ≡ a (mod p). On aura donc ici d=43, car 43×3 ≡ 1 mod(64).
On a donc une clef publique (e, n) avec e=3 et n=85 et une clef privée (d, n) avec d=43 et n=85.
Pour rester simple, on va dire que le message que Bob souhaite envoyer à Alice est le nombre 10. Il faut que ce nombre soit inférieur à n, ce qui est bien le cas ici. On notera ce nombre M.
Pour chiffre son message, Bob va utiliser la clef publique d’Alice (qui contient e=3 et n=85) et calculer C = Me mod(n), ou C est le message chiffré qu’il enverra à Alice. Ici, C=103 mod(85) = 65.
Il envoie donc 65 à Alice. Pour décoder ce 65 et retrouver le 10 original, Alice calculera M = Cd mod(n), ce qui nous donnera M = 6543 mod(85), ce qui donne bien 10.
Voici une petite application qui vous permettra de tester avec vos propres données.
Attention, ici c’est un exemple très simplifié, on a juste vu le principe, mais un vrai chiffrement RSA est plus complexe que ça. Il utilise des clef d’une taille énorme, il travaille en binaire, on choisit e d’une façon plus intelligente, etc.
Voici par exemple un nombre premier utilisé pour p ou q dans une version normale 2048 bits de RSA :
139903732236291453096811051973971311924811662360692348316347747578574483498591281047941918591784212013418326248739596767755702817512516663031064048130004928580247473152237195841354120301859017879901683238347321315368776622689785726469043957211545880561996677382845047621692219334239673968921471463923176364891
L’exposant privé (d) comporte typiquement environ 600 chiffres décimaux.
